These will be my notes on back-propagation. neptune
Intro
To train a neural network, there are 2 phases (phases).
- Forward
- Backward
In the forward pass, we start by propagating the data inputs to the input layer, go through the hidden layer(s), measure the network’s predictions from the output layer, and finally calculate the network error based on the predictions the network made.
The network error measures how far the network is from making the correct prediction.
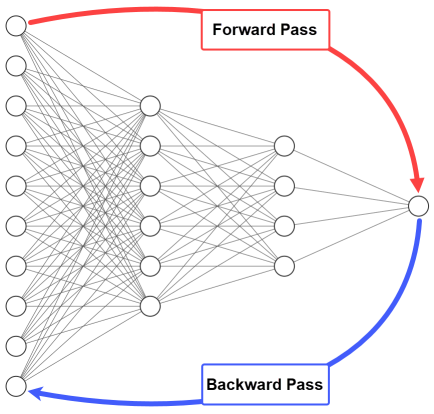 In the backward pass, the flow is reversed so that we start by propagating the error to output layer reaching the input layer passing through the hidden layer(s). There are a set of steps used to update network weights to reduce the network error.
In the backward pass, the flow is reversed so that we start by propagating the error to output layer reaching the input layer passing through the hidden layer(s). There are a set of steps used to update network weights to reduce the network error.
Why use the back-propagation algorithm
If the network error is high, the network didn’t learn properly from the data. It indicates that the current set of weights isn’t accurate enough to reduce the network error and make accurate predictions.
Some advantages of using the back-propagation algorithm.
- It’s memory efficient, especially relative to other optimization algorithms
- Very fast, for small and medium-sized networks
- Generic enough to work with different network architectures like neural networks, generative adversarial networks, etc.
- There are no parameters to tune the algorithm, so there’s less overhead
Using the back-propagation algorithm, we can know how each single weight correlates with the error. This tells us the effect of each weight on the prediction error.
Interpreting results of back-propagation
There are two useful conclusions from each of the last two derivatives. These conclusions are obtained based on:
- Derivative sign
- Derivative magnitude (DM)
If the derivative sign is positive, that means increasing the weight increases the error. In other words, decreasing the weight decreases the error.
If the derivative sign is negative, increasing the weight decreases the error. In other words, if it’s negative then decreasing the weight increases the error.
But by how much does the error increase or decrease? The derivative magnitude answers this question.
For positive derivatives, increasing the weight by p increases the error by DMp. For negative derivatives, increasing the weight by p decreases the error by DMp.
Drawbacks of back-propagation
- Considers all neurons in the network equally and calculates their derivatives for each backward pass
- relies on infinitesimal effects
- error function and activation function must be differentiable
- in the forward pass, layer i+1 must wait the calculations of layer i to complete. In the backward pass, layer i must wait layer i+1 to complete